 |  |  |
With the beginning of our Spring Break, I've been able to update the Multiplication Strategy Posters I made for my classes, and get them ready to put on-line. If you click the pictures above, you'll be taken to Teachers Pay Teachers, where you can download these posters FREE (just like the subtraction and addition strategy posters).
There are 3 different sets to choose from, depending on where the children in your class are with their understanding of multiplication. I often had 2 sets displayed simultaneously. It's rare to have a class where all of the children are working at the same level, which is why I ended up making 3 different versions.
These posters provide visual support for children as they develop their understanding of different strategies for solving multiplication equations. They can also support your own understanding (this was my own experience!) which will enhance your ability to transcribe children's mathematical thinking for the rest of your class during Number Talks.
It can be particularly tricky to help children understand what is happening when they use 'Factoring', 'Partial Products' and 'Double and Half'. Often, children will use these strategies without completely understanding why they work. These posters provide a visual representation of what is happening when you use these strategies - I've always found that these types of representations help both me AND my class to deepen our understanding of the mathematical processes we are using.
There are 3 different sets to choose from, depending on where the children in your class are with their understanding of multiplication. I often had 2 sets displayed simultaneously. It's rare to have a class where all of the children are working at the same level, which is why I ended up making 3 different versions.
These posters provide visual support for children as they develop their understanding of different strategies for solving multiplication equations. They can also support your own understanding (this was my own experience!) which will enhance your ability to transcribe children's mathematical thinking for the rest of your class during Number Talks.
It can be particularly tricky to help children understand what is happening when they use 'Factoring', 'Partial Products' and 'Double and Half'. Often, children will use these strategies without completely understanding why they work. These posters provide a visual representation of what is happening when you use these strategies - I've always found that these types of representations help both me AND my class to deepen our understanding of the mathematical processes we are using.
 |  | Keeping in mind that there are 3 different sets of posters (so you can choose the set or sets that are appropriate for your class), you can see to the left the |
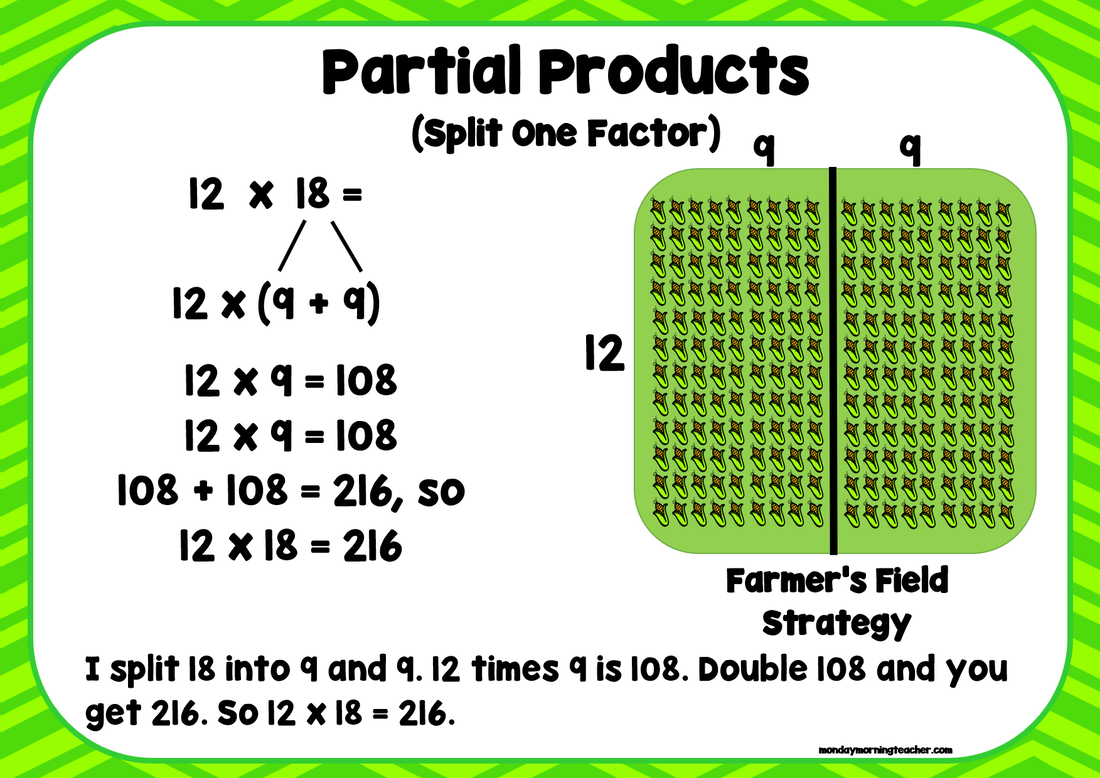
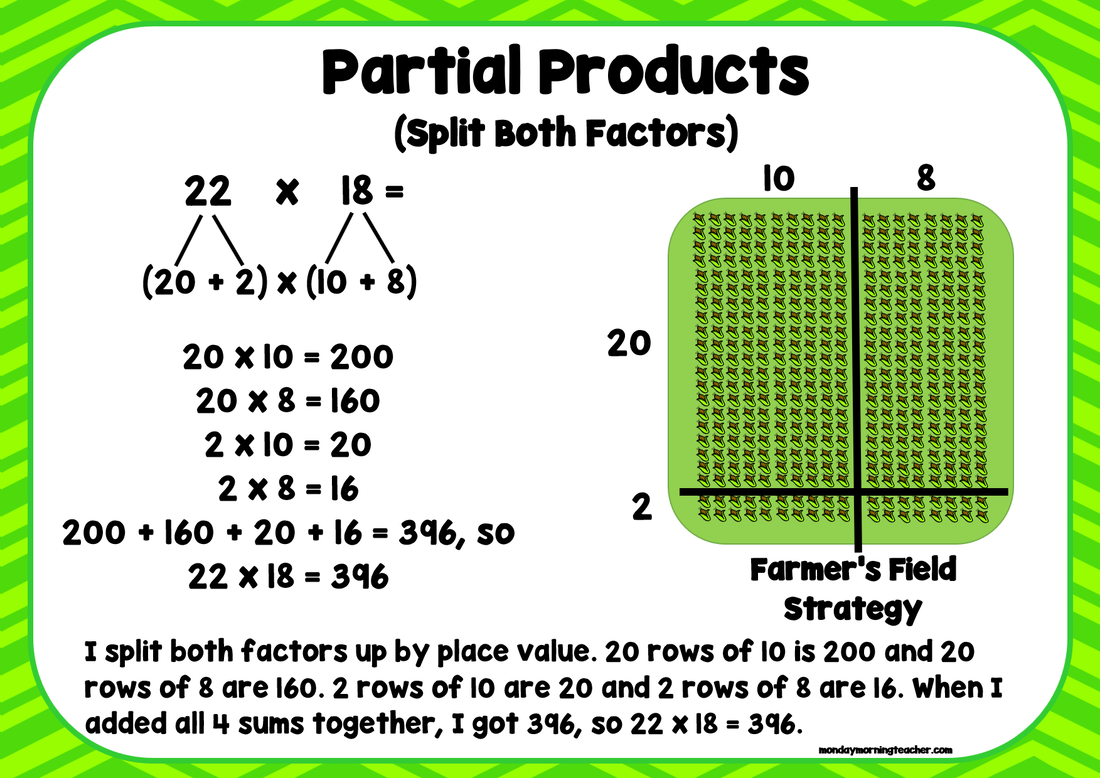
2 different 'Partial Products' strategy posters from the most advanced set of posters (example equations in this set ask children to multiply 2 digits by 2 digits). Children often become confused by which numbers to multiply by each other when they split one factor versus when they split 2 factors. These posters provide clear pictures of what is happening mathematically when children use these strategies. The posters also give a context (a farmer's field!) that helps the children to remember how and why the strategy works.
 |  |
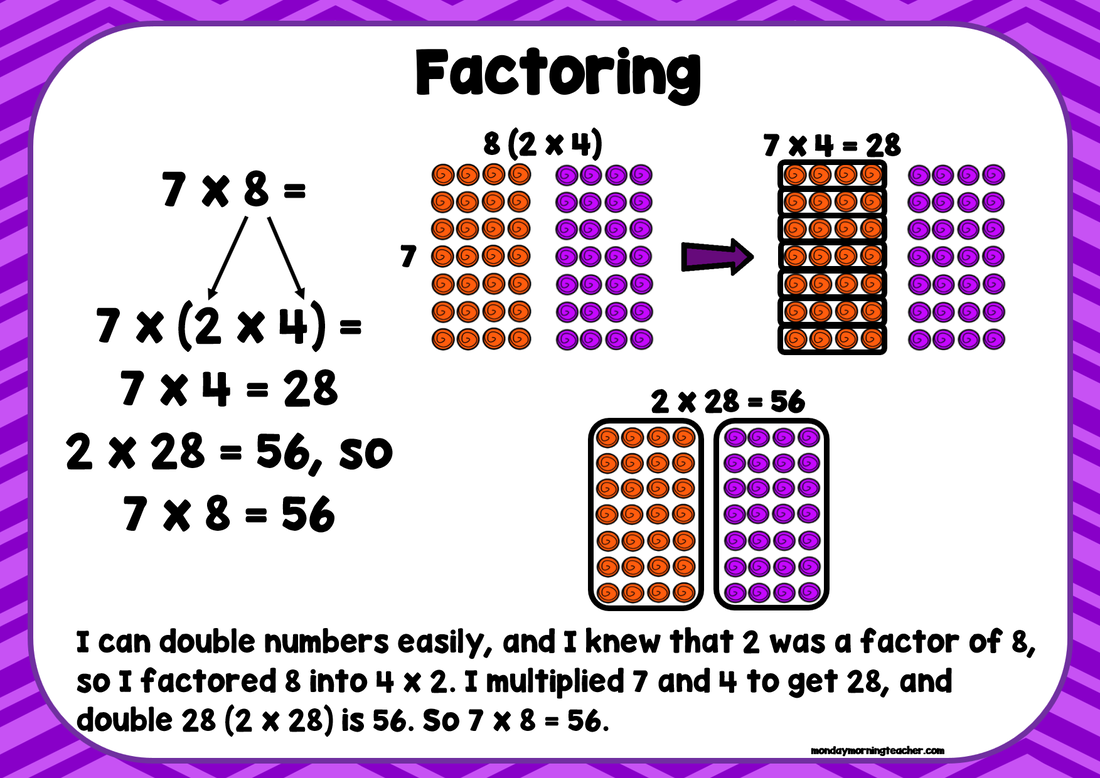
Another tricky distinction children need to understand is the difference between 'Partial Products' and 'Factoring'. The 2 posters above are taken from the easiest poster set (all example problems in this set are taken from within the Times Tables that children are asked to memorise), but they illustrate the difference between these 2 strategies. With partial products, one or both factors are split using addition. Smaller/easier multiplication sums are completed (in the example above, 4x5 and 4x4), and the resulting answers are added together to get a final answer. This can be explained using an area model (or my 'Farmer's Field').
When students 'factor a factor' to solve their equation, they are re-arranging the multiplication groups. They are NOT splitting the factors by addition - they are reducing the factors in their original problem to smaller factors. So - instead of having '7 rows of 8' (in the poster above), that can be turned into '7 rows of 4' (as 8 = 2 rows of 4). Once you have found that '7 rows of 4' is 28, you have 2 groups of 28 (2 x 28), which gives you your final answer of 56. When you factor the original factors, all of the factors are then multiplied by each other BECAUSE you are re-arranging the groups/rows that you are working with in multiplication. This strategy is tricky, and younger students are unlikely to use it. But as children get older, if they can begin to understand and use this strategy, they will find it extremely helpful as they move into working with algebraic equations.
These files also include easier/more straightforward strategies (which the children in your class may be more likely to use):
When students 'factor a factor' to solve their equation, they are re-arranging the multiplication groups. They are NOT splitting the factors by addition - they are reducing the factors in their original problem to smaller factors. So - instead of having '7 rows of 8' (in the poster above), that can be turned into '7 rows of 4' (as 8 = 2 rows of 4). Once you have found that '7 rows of 4' is 28, you have 2 groups of 28 (2 x 28), which gives you your final answer of 56. When you factor the original factors, all of the factors are then multiplied by each other BECAUSE you are re-arranging the groups/rows that you are working with in multiplication. This strategy is tricky, and younger students are unlikely to use it. But as children get older, if they can begin to understand and use this strategy, they will find it extremely helpful as they move into working with algebraic equations.
These files also include easier/more straightforward strategies (which the children in your class may be more likely to use):
 |  |
I hope you find some (or all) of these poster sets useful. In the first set, the example equations are all taken from the times tables (2-12) that children are asked to memorise. In the second set, the example equations are all '1 digit x 2 digit'. In the final set, the example equations are '2 digit x 2 digit'.
Happy Multiplying!
Happy Multiplying!
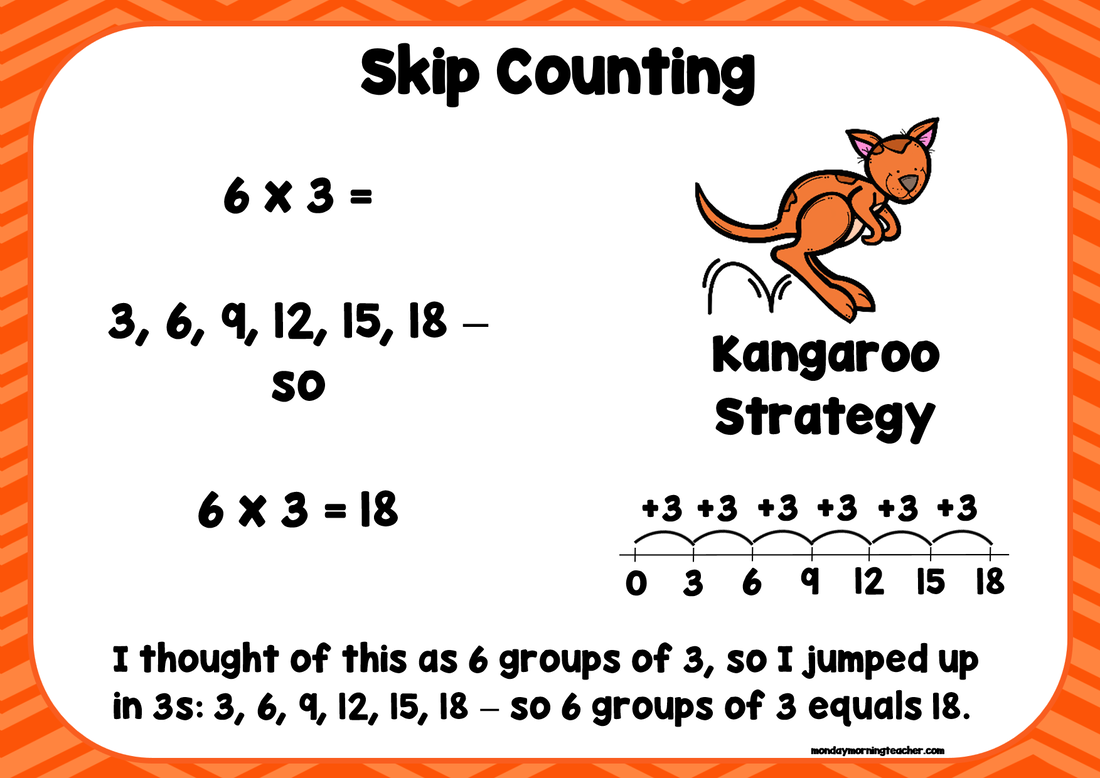
RSS Feed