
I wanted to share another one of those moments - I hope that these stories might encourage you to give number talks a try (and persevere with them!) in your own classroom.
Division is a tricky operation. When you google Number Talks on youtube, the division number talks are few and far between - perhaps we teachers aren't quite sure enough of our own grasp of this operation to want to allow others to observe us when we are exploring it with our classes.
But if you are willing to take the chance, your class will rise to the challenge (even if you yourself have a few stubbles along the way - that's OK and part of the learning process).
This past year, I had a student teacher who was doing a division number talk. She chose the equation given above. The class found this pretty straightforward, and the first kid to defend the answer '4', gave a standard 'think multiplication' strategy: they knew that 4 x 10 was 40, so 40 divided by 10 was 4. Fair enough.
Then another child offered to give a different strategy. He said that he knew that 40 divided by 5 was 8, because 8 groups of 5 are 40. BUT - if you double the number of groups you have (from 5 to 10), then you must half the number of things in each group (from 8 to 4) - so because he actually needed to divide by 10 (rather than 5), he knew he needed to half 8 to get 4.
Did you follow that? Because my student teacher struggled to. I knew intuitively when the child offered this explanation that he was right (and that his strategy would always work), but I would have struggled to articulate it at the time. So we congratulated the pupil on his thinking, agreed to come back to it later, and moved on.
My student and I then sat down with manipulatives after school to figure out exactly what this pupil had known instinctively! If you found it difficult to follow the strategy as I explained it, get out manipulatives as well, and you'll soon see what he did (this need to use manipulatives as a teacher, in order to really understand some of the different strategies, has been a very helpful reminder for me that our children MUST have many repeated concrete experiences with mathematical concepts in order to internalise and understand them before they move to working with the abstract equations alone).
Once you've followed what this pupil did (and if you didn't need to use manipulatives, I'm very impressed!) how does this strategy help our classes with division? My student's initial reaction (once we'd figured out what he did) was that this pupil took an easy problem and solved it in a more difficult way.
BUT - if we understand this strategy, we can use it whenever we are asked to divide by 5. And it makes division by 5 a very simple mental operation - no need for paper ever again. You can see this in the picture below:
Not every child in your class will follow every strategy that other children are using. But with repeated exposure to different ways to manipulate equations, as well as repeated hands-on experience of solving equations using manipulatives so that they can see how different strategies work, your class will learn to think and reason mathematically. They won't always need to wait for you to explain how to do something - they will have the confidence to approach a problem and figure out how to solve it for themselves.
Give it a try (but maybe don't start with division!).


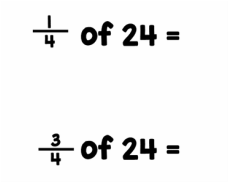







 RSS Feed
RSS Feed