As we come to the end of the year, I've been thinking about how I've used number talks in my class this year. As I moved from Primary 1 (kindergarten) last year to Primary 3 (2nd grade) this year, it has been a bit of a challenge at times. Why? Because my understanding of mathematics is largely procedural. I can look at a problem and follow the algorithm I was taught years ago and get the right answer. BUT - I often have only a vague understanding of why the algorithm works. And I definitely struggle to 'think outside the box' and solve problems in ways I wasn't taught.

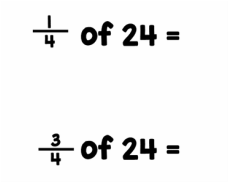
This year, I've found that I've needed to work hard (and pull out concrete materials to aid my own understanding of why a given strategy works!) to really understand what is happening when I use the multiplication algorithm, for example. Or how I can split numbers apart and combine them in different ways to mentally solve problems that the 2nd grade me would have definitely used paper, pencil and algorithm for.

​I think this is the main reason why number talks can be daunting for teachers at first - we are asking our kids to reason about mathematics that we might find just a little bit tricky ourselves (luckily, I've only been teaching Primary 3!). And what if the kids come up with a strategy that we can't follow, or that we can't make clear to the rest of the class? I benefited, I think, from starting the Number Talk process in kindergarten, so the different strategies I was getting my head around were simple.

​But when you teach this way, you really open up an exciting mathematical world for your pupils. As the year has progressed, I've often found myself thinking that some of my class have a much better intuitive grasp of mathematical fundamentals than I have (oops). They can reason with numbers in a way that often just never occur to me.

​Take as an example, the 2 fraction equations given above. I put the first equation to my class yesterday morning, and many of the kids were able to tell me that the answer was '6'. To help, I put up 24 different magnetic cubes, and we split them up into our 4 groups, so we could all see the 6 cubes in each group.

​Then we moved to the second equation. Again, a reasonable number of children could tell me that the answer was 18 (although this concept is definitely trickier for a lot of them!). But when I asked one little boy to defend his answer, this is what he told me:

​I knew that 1/4 of 24 was 6, and I had 3/4 left, so I took 1/4 (which is 6 cubes) away from 24 to get 18.

​Oh, My. Goodness. Of course - how simple. But it never in a million years would have occurred to me.

​Implementing number talks can be tricky. And you will definitely stretch your own understanding of mathematical processes as you implement them. But the rewards for your pupils are amazing, so I would really encourage you to give it a try. Start simple - even if you are teaching an older class, if they aren't familiar with number talks and having to explain their mathematical thinking, they will thank you (and you will thank yourself!) for starting slowly. But give it a try - you won't regret it.

I've joined an international on-line book study of the book 'Making Number Talks Matter', and we've just finished thinking about chapter 1.

I've been doing number talks with my classes for the past year and a bit. I think they are the single most effective way we as teachers can help our classes develop number sense, fact fluency, and fluency with computation strategies. They really do make that much difference, in my experience. 

Along with number talks, I'm also a fan of JUMP maths. The founder of JUMP maths, John Mighton, is convinced that we can narrow the achievement gap between our most and least able maths students by making sure that mathematical ideas are broken down into small, understandable steps.

For me, number talks is a huge part of 'breaking down concepts' for children, so that the concepts are accessible to everyone, and not just the children who 'get' maths intuitively. Except teachers aren't the ones breaking the concepts down - children are doing that for themselves, as they reason about numbers, share their reasoning with their classmates, or explain the computation strategies used by someone else. We know that children learn and retain the most when they are teaching others. Number talks expect them to do just that - in a very real sense, our students teach each other, as they explain the strategies they have used to solve the problems we pose.

We've all had children in our class who just seem to 'get' maths - everything about numbers comes intuitively to them. Conversely, we've all also had children who seem to struggle with even simple mathematical concepts. In my brief experience with number talks, I've found that they allow the children who struggle to access numbers in a powerful way. ​​ And when we expect ALL of our children (and not just the high fliers) to articulate their mathematical thinking, we send an equally powerful message about their capabilities and our faith in their capabilities.

Number talks empower our students in maths. They take a subject that children are often afraid of, and turn it into something they teach! I love the excitement of children desperate to share with the class 'how they got the answer'. These kids are desperate to teach their classmates, when we provide the structure and setting through number talks. No wonder ​​this is such a powerful mathematical routine. I'm looking forward to digging a bit deeper over the next few weeks of the book study.

​ ​​

All of my Grade 2/Primary 3 number talks focus on addition and subtraction. But I know I'll have kids my class who are already proficient with their multiplication tables and early division, so I was thinking ahead to that a bit.

Having a look online, I found this article 'Number Talks Build Numerical Reasoning' by Sherry Parrish (author of Number Talks). It gives an illustration of a 4th grade (Primary 5) multiplication number talk - well worth a read to see if you can follow the mathematical thinking of this group of 9 year olds! This is the kind of thinking with numbers that I want to be developing in my own class.

This past year in Primary 1 (kindergarten), I've had dot cards and rekenreks readily available, so number talks have been easy to implement. I've realised, however, that I've done them randomly - I haven't followed the suggested sequences from the book.

I feel like the kids in my class benefited enormously from the number talks, and I was pleased with how their number sense developed over the year. Re-reading the book, however, I can see benefits of following the sequences given in the book - not least because it means I don't have to think on my feet nearly as much!

But it isn't very practical to have the book open next to you while you are teaching, so my daughter and I put our heads together to come up with a better way to approach this.

My very kind daughter photocopied all of the pages which give 2nd grade (Primary 3) number talk sequences. Each square you see on the page contains a sequence of 4 different equations which would be given one after another, to help the children focus in on using a given computation strategy.

We enlarged the page from A4 to A3 (not sure what that translates to on American photocopiers), to make the squares slightly larger. This summer, my daughter has been cutting out the cards for me, keeping each group of talks together (each page represents a group of talks). One page might be 1-2 weeks worth of number talks for your class, depending on how quickly they were picking up the strategy you were working on.

What to do next? Well, if you were to wander through my classroom, and have a look at the different resources available for the kids, you would quickly realise that I LOVE scrapbooking rings. So I obviously thought of them again when we were thinking about how to make it easy to sequence number talks effectively in the classroom.

Here, you can see the different sets of number talks that my daughter has cut out (all bundled together with rubber bands). Next to the unfinished sets is a set I've put onto a scrapbooking ring - I've ordered the cards in the same order given in the Number Talks book. The green card on the ring is my 'go' card - it lets me know that the following card is the first card in my number talk sequence.

Once these sets are all made up, I'll still have a bit of thinking to do. I suspect I'll need to add handwritten labels to the green card, giving the strategy those number talks are targeting. I'll also probably need to number them, so I have a rough idea of the general order (although I'm not above mixing things up a bit, if that seems like the right thing to do for my class!). Once we're further along in getting these ready for next year, I'll post more pictures and let you see how they've all turned out.

I bought Number Talks last summer, because I wanted to re-think how I taught maths. It has been a revelation, and now I can't imagine teaching maths without using the strategies and techniques in this book.

We all work to help our classes develop number fluency and the ability to use different computation strategies. In Number Talks, the emphasis is on children talking about how they solved a problem. Many of us probably grew up being told to 'show your work' in maths - with number talks, children 'talk through their work' - which allows them to clarify their own thinking, become the mathematical experts for their own class, and help their classmates see different ways of arriving at the right answer.

The following video shows a kindergarten/Primary 1 number talk, given by the same teacher who presents the kindergarten number talk in the Number Talk book. If you've read my post about developing Number Sense, you'll realise how many elements of the Number Talk routine I've borrowed in my own teaching!

In my Primary 1 class, we've done many number talks using dot cards. In our routine, when I listen to the children's explanations for how they saw a given number, I write up the corresponding number sentence on the white board. In the above clip for the dot card showing '10', for example, when the girl said she 'just counted', I would write 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 10. Another boy saw two 5s and knew that was 10, so 5 + 5 = 10 would be written up, too. Number talks designed for older children begin with the written mathematical sums, but I like connecting the written notation to their dot card subitising skills. I think it helps my littlies to connect the representation of a number (the dot card picture) to its abstract mathematical formulation (e.g., 5 + 5 = 10). They can also see very quickly that there are slower vs. more efficient ways to count/add numbers!

Has anyone else read Number Talks and implemented ideas from it in your own class? I'd love to hear about your experiences.